1D Target (Stop Sign)

This module is the setup for a simple vehicle driving in a straight line. The goal is to stop before some target stop sign. The following figures for acceleration and velocity demonstrate how realistic demonstrations contain a significant amount of variation and error:

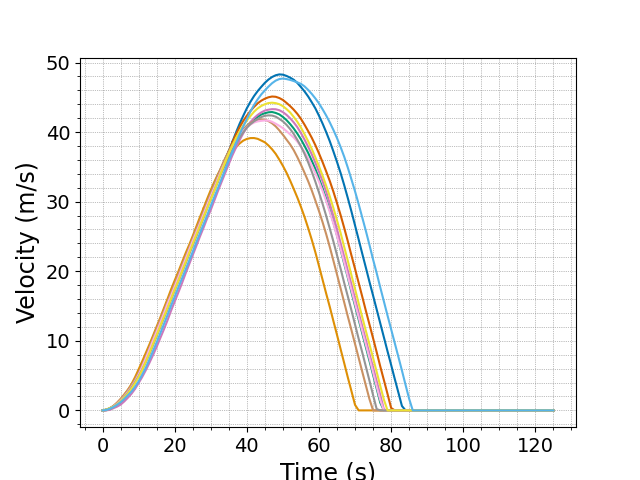
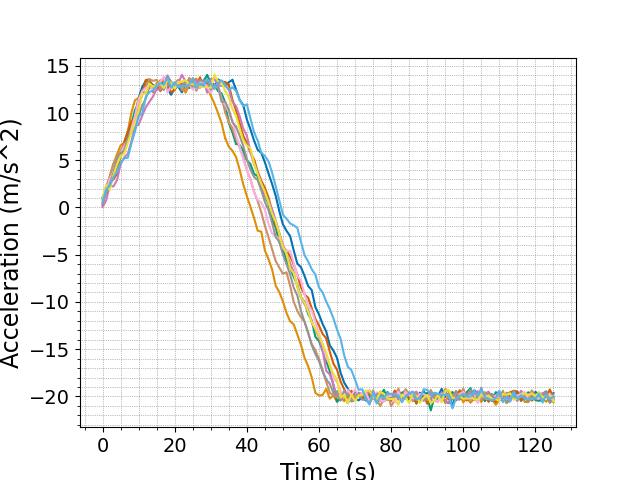
Try running the algorithm on the setup by running make and make emng (or see snapshots/ for a selection of pre-acquired results).

The most useful/informative outputs will be:

• out/aspx/, which stores the synthesized policies. For example, we can see the final policy (which we have cleaned up here for presentation):

   if ha == ACC and flp(lgs(Minus(v, v_max), -0.456573, 1.388253)):
       return CON
   if ha == ACC and flp(lgs(Minus(dns, DistTraveled(v, a_min)), -6.926392, -2.609171)):
       return DEC
   if ha == CON and flp(lgs(Minus(DistTraveled(v, a_min), dns), -2.829544, 0.814321)):
       return DEC
   return ha
  

• plots/accuracy.png and plots/likelihoods.png, which shows the progress of the EM loop across iterations. Here is a (slightly prettified) version for this task:

  

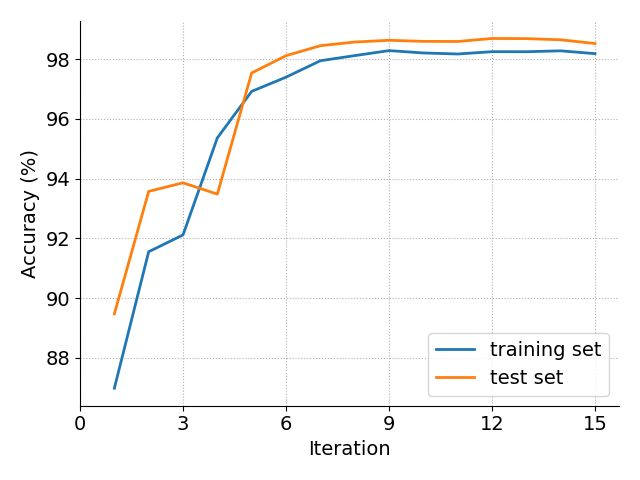
• plots/testing/xx-x-graph.png, which gives a visual representation of the action labels selected by the policy on the testing set. The first number in the file name indicates the iteration. For example:

  Iteration 1:

  

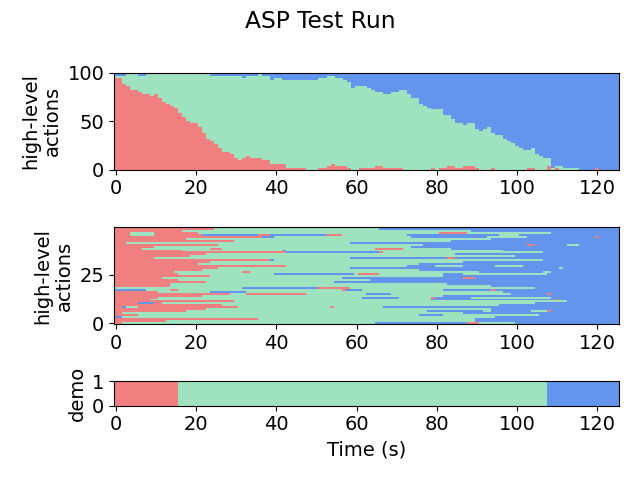
  Iteration 2:

  

  Iteration 9:

  

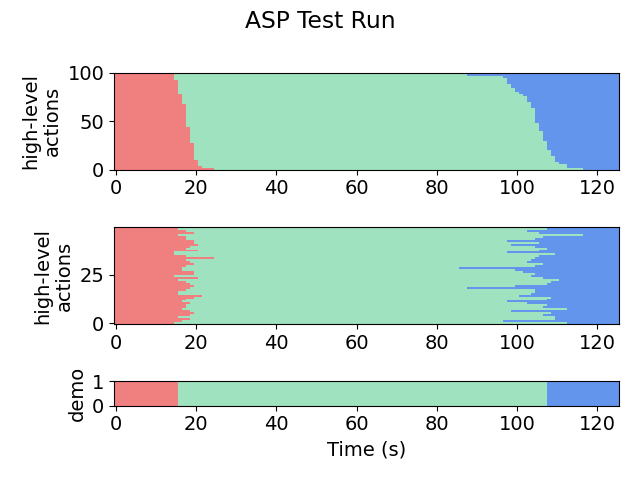
• plots/testing/LA-xx-x-graph.png, which gives a visual representation of the low-level observations predicted by the policy on the testing set. For example, here is iteration 9:

  

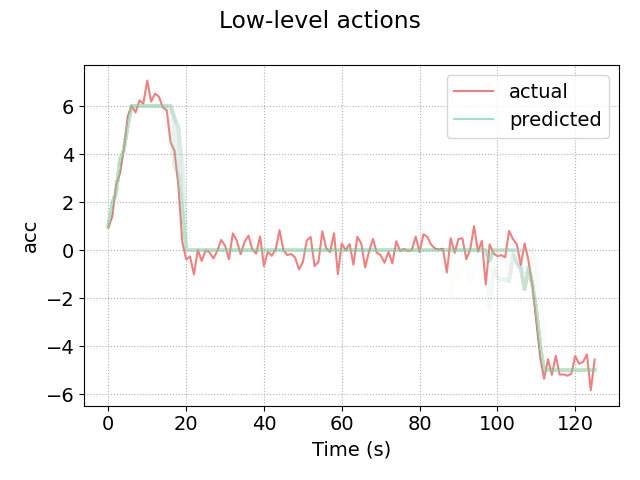
Other outputs include:

• sim/ - contains the simulated trajectories for each robot
• out/aspx/ - contains the synthesized program at each iteration
• out/examples/ - contains the particle filter outputs at each iteration, in csv format
• out/states/ - contains pure ASP outputs, in csv format (i.e. the action labels acquired by running the given ASP at each time step)
• plots/ - contains plots of trajectories for pretty viewing

We provide the observation model below:

step(action):
    if (action == ACC)
        acc = min(acc+1, acc_max)
    else if (action == DEC)
        acc = max(acc-1, acc_min)
    else if (action == CON)
        if (acc < 0) acc = min(acc+1, 0)
        else acc = max(acc-1, 0)